ECMAScript 6 Proper Tail Calls in WebKit

Proper Tail Calls (PTC) is a new feature in the ECMAScript 6 language. This feature was added to facilitate recursive programming patterns, both for direct and indirect recursion. Various other design patterns can benefit from PTC as well, such as code that wraps some functionality where the wrapping code directly returns the result of what it wraps. Through the use of PTC, the amount of memory needed to run code is reduced. In deeply recursive code, PTC enables code to run that would otherwise throw a stack overflow exception.

What is a Proper Tail Call?

Typically when calling a function, stack space is allocated for the data associated with making a function call. This data includes the return address, prior stack pointer, arguments to the function, and space for the function’s local values. This space is called a stack frame. A call made to a function in tail position will reuse the stack space of the calling function. A function call is in tail position if the following criteria are met:

The calling function is in strict mode.
The calling function is either a normal function or an arrow function.
The calling function is not a generator function.
The return value of the called function is returned by the calling function.

When a function call is in tail position, ECMAScript 6 mandates that such a call must reuse the stack space of its own frame instead of pushing another frame onto the call stack. To emphasize, ECMAScript 6 requires that a call in tail position will reuse the caller’s stack space. The calling function’s frame is called a tail deleted frame as it is no longer on the stack once it makes a tail call. This means that the tail deleted function will not show up in a stack trace. It is important to note that PTC differs from Tail Call Optimization, which is a discretionary optimization that many optimizing compilers will make for various performance reasons.

Benefits of Proper Tail Calls

PTC was added to ECMAScript primarily to reuse stack space. The reuse of the stack memory allows for recursive and tail call coding patterns common to functional programming and other programming paradigms. Using PTC, a program could make an unbounded number of consecutive tail calls without unboundedly growing the stack.

PTC provides other benefits as well. Programs that utilize PTC can see a reduced memory footprint because the garbage collector will be more likely to collect certain local objects. Programs that utilize PTC can also see an improvement in speed because there is less processing when returning from a tail called function.

Stack Space

Reduced stack usage can provide benefits in other ways as well. Modern computing devices incorporate tiered memory caches to reduce latency in memory accesses. Although these caches are generous in size, they are still finite. Reducing stack usage through the use of PTC also reduces the amount of cache space needed, freeing up cache space for other memory accesses.

Locally Allocated Objects

Consider a function that allocates a local object, but that object is never made visible to other code. The only references to such a local object will be through a pointer in the function’s stack frame or in a register that the function is using. Should the JavaScript virtual machine need to garbage collect memory, it will find a reference to such a local object by scanning the stack and the contents of the CPU’s registers. If that function makes a call to another function and that call is not a tail call, then any local objects of the calling function will not be collected until the calling function itself returns. However, if a function makes a tail call to another function, all local objects of the calling function can be garbage collected because there are no more stack references to the object.

Returning from a Tail Called Function

Another benefit of PTC is that when a leaf function returns, it bypasses all intermediate tail called functions and returns directly to the first caller that didn’t make a tail call. This eliminates all of the return processing of those intermediate functions. The deeper the call chain of successive tail calls, the more performance benefit this provides. This works for both direct and mutual recursion.

Examples

There are many algorithms that are best written using recursion. Many of those algorithms naturally take advantage of PTC, while others may require some reworking. Consider writing a program to compute the greatest common divisor (GCD) function using Euclid’s algorithm. The translation of Euclid’s algorithm into a program that utilizes PTC is simple, elegant, and natural:

"use strict";
function gcd(m, n)
{
    if (!n)
        return m;
    return gcd(n, m % n);
}

The natural translation of other recursive mathematical functions can lead to recursive calls that are not in tail position. For example, a program that computes factorial (N!) is commonly written as:

"use strict";
function factorial(n)
{
    if (!n)
        return 1;
    return n * factorial(n - 1);
}

In this function, the recursive call to factorial() is not in tail position because the return statement computes and returns the product of n and the result of the recursive call. As a reminder, to be in tail position, the return value of the called function must be the only thing returned by the calling function. With a little modification, we can rewrite factorial to utilize PTC as follows:

"use strict";
function factorial(n, partialFactorial = 1)
{
    if (!n)
        return partialFactorial;
    return factorial(n - 1, n * partialFactorial);
}

This change puts the recursive call to factorial in tail position which allows the function to take advantage of PTC. The number of recursive calls and arithmetic operations is the same for both versions.

This next example involves the functions computeSquareRoot(), computePositiveSquareRoot() and iterativeSquareRoot() which are used to calculate the square roots of numbers using Newton’s Iterative method:

"use strict";
function computeSquareRoot(x)
{
    if (!x)
        return "0";

    let imaginaryPart = "";
    if (x < 0) {
        x = -x;
        imaginaryPart = "i";
    }

    return computePositiveSquareRoot(x).toString() + imaginaryPart;
}

function computePositiveSquareRoot(x)
{
    let targetEpsilon = x / 10000000000;
    return iterativeSquareRoot(x, x / 2, targetEpsilon);
}

function iterativeSquareRoot(x, estimate, targetEpsilon)
{
    let newEstimate = ((x / estimate) + estimate) / 2;
    let delta = Math.abs(estimate - newEstimate);

    if (delta <= targetEpsilon)
        return newEstimate;

    return iterativeSquareRoot(x, newEstimate, targetEpsilon);
}

The top function, computeSquareRoot(), determines if the result will be a real or imaginary number and then calls computePositiveSquareRoot(), which sets up the iterative square process and returns the result of iterativeSquareRoot(). The call to computePositiveSquareRoot() in computeSquareRoot() is not in tail position since additional processing is done on the result of the call. All other function calls are tail position.

Suppose computeSquareRoot() is called with 99 as the argument. It will call computePositiveSquareRoot(99), which will subsequently call iterativeSquareRoot(99, ...). Using Web Inspector, we observed that iterativeSquareRoot() calls back to itself 6 times before returning a result. That result is returned directly back to computeSquareRoot, where it is converted to a string, saving the processing of 7 returns.

This last example shows the type of functional programming that PTC enables:

"use strict";
function newList(count)
{
    let head = { value: count, next: null };
    while (--count)
        head = { value: count, next: head };
    return head;
}

let count = 100000;
let list = newList(count);

function contains(list, x)
{
    if (!list)
        return false;
    if (list.value == x)
        return true;
    return contains(list.next, x);
}
...

if (contains(list, someValue))
   ...

The function contains() searches the list using tail recursion. For a list the size of 100,000 elements given in this example, most browsers will run out of stack memory and throw an exception. In strict mode, where contains() can take advantage of PTC, the program runs just fine. It is also interesting to note that even with a list size small enough to allow this code to run without PTC, using PTC results in the code running 2.5x faster.

Things to Note

There are a couple subtle, but minor issues to be aware of when using PTC. Remember that PTC is only available in strict mode and only for calls made from tail position. The other notable change involves the generation of stack traces. There are some non-standard ECMAScript features in JavaScript that work differently in the presence of PTC. These include Error.stack and the Console object’s stack trace. For example, say a tail called function gonnaThrowAnError() throws an Error object; the function that catches that Error will not see the function that called gonnaThrowAnError() in the Error object’s stack trace. As a general rule, the Console object’s stack trace will not include a function that made a tail call to another function. We call such frames tail deleted frames because its as if they are deleted from the stack when making a call.

Debugging PTC with ShadowChicken

Because PTC places a strict resource guarantee on stack usage, JavaScriptCore cannot keep around information for all tail deleted frames. Keeping around any extra resources, no matter how small, for an unbounded number of tail deleted frames is not possible because it could use an unbounded amount of memory and eventually exhaust the memory limits of the program. Given that tail calls do not keep around any information in the program’s executing state, debugging tail calls can be challenging when using an interactive debugging tool. Without any added machinery, the debugger will not know if a tail call did or did not occur. Because we want to make debugging tail calls inside Web Inspector a great experience, we have implemented mechanisms inside JavaScriptCore to keep around a shadow stack that will display a finite number, currently 128, tail deleted frames. This allows us to both provide strict guarantees on memory usage and to provide users of PTC the benefit of seeing the most important stack frames in their program inside Web Inspector.

We call our shadow stack implementation ShadowChicken. The name is an homage to the CHICKEN scheme interpreter. ShadowChicken uses a logging mechanism for constructing its shadow stack. The log works as follows:

On entry to a function, the function’s callee will log a prologue packet.
When making a tail call, the caller will log a tail packet just before the tail call occurs.
When an exception is thrown, ShadowChicken will log a throw packet.

To construct the shadow stack, ShadowChicken takes two inputs:

The log filled with a sequence of prologue, tail, and throw packets.
The current top of the machine stack (note that the machine stack does not contain any frames that are tail deleted).

Given these two inputs, ShadowChicken is able to construct a shadow stack that includes tail-deleted frames. It will reconcile the machine stack with its log. Because the log has tail packets for when tail calls occurred, it is able to use the log to insert tail-deleted stack frames into the shadow stack to represent frames that were only present on the machine stack before a tail call occurred. ShadowChicken uses a constant amount of memory on top of the memory your program already uses. The log is fixed in size. Whenever ShadowChicken runs out of space in the log, it will perform its reconciliation algorithm to update its internal data structure about the state of the shadow stack. The shadow stack will contain at most 128 tail deleted frames, a number we believe strikes a good balance between programs that intentionally take advantage of PTC and programs that just happen to use PTC without the explicit intention of doing so.

Hooking Up ShadowChicken to Web Inspector

Because JavaScriptCore has the machinery for constructing a shadow stack, Web Inspector can use JavaScriptCore’s shadow stack in its debugger. This allows users of Web Inspector to interact with tail deleted stack frames as if they are real stack frames that are on the current machine stack.

Let’s see some interactions with Web Inspector and the iterative square root code to compute the square root of 99. After setting a breakpoint in iterativeSquareRoot() and invoking computeSquareRoot(99), Web Inspector shows that we are paused, ready to return the result.

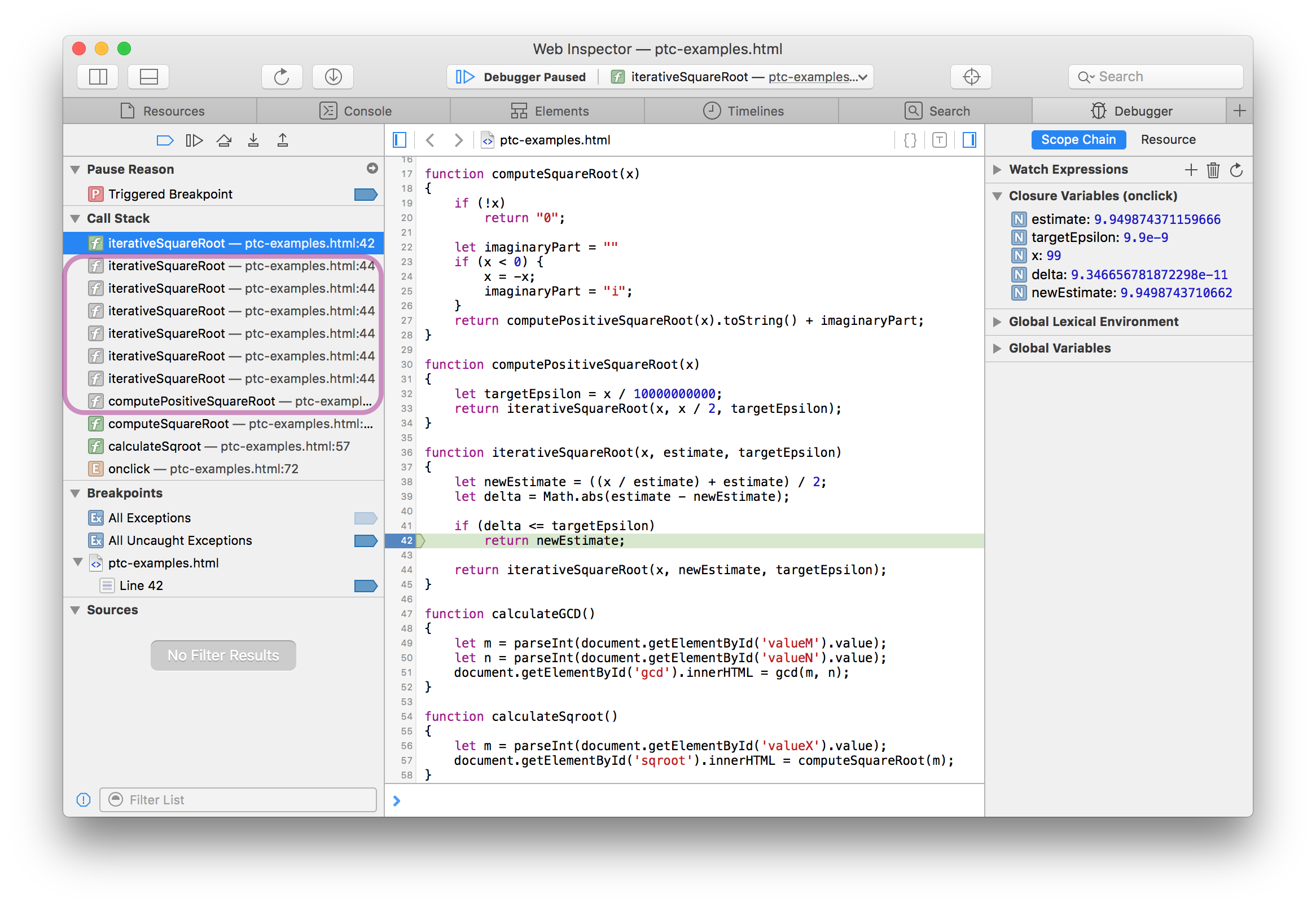
Breakpoint with tail deleted frames in the stack.

Web Inspector not only shows the frame we’re stopped in and the original caller, computeSquareRoot(), but also shows the seven tail deleted frames. These are highlighted in the above image. Tail deleted frames in Web Inspector show up with a gray ƒ icon to their left. As the next image shows, the variables in tail deleted frames can be examined as if the frame were a normal frame. The next image shows Web Inspector inspecting a tail deleted frame one level up from the leaf frame.

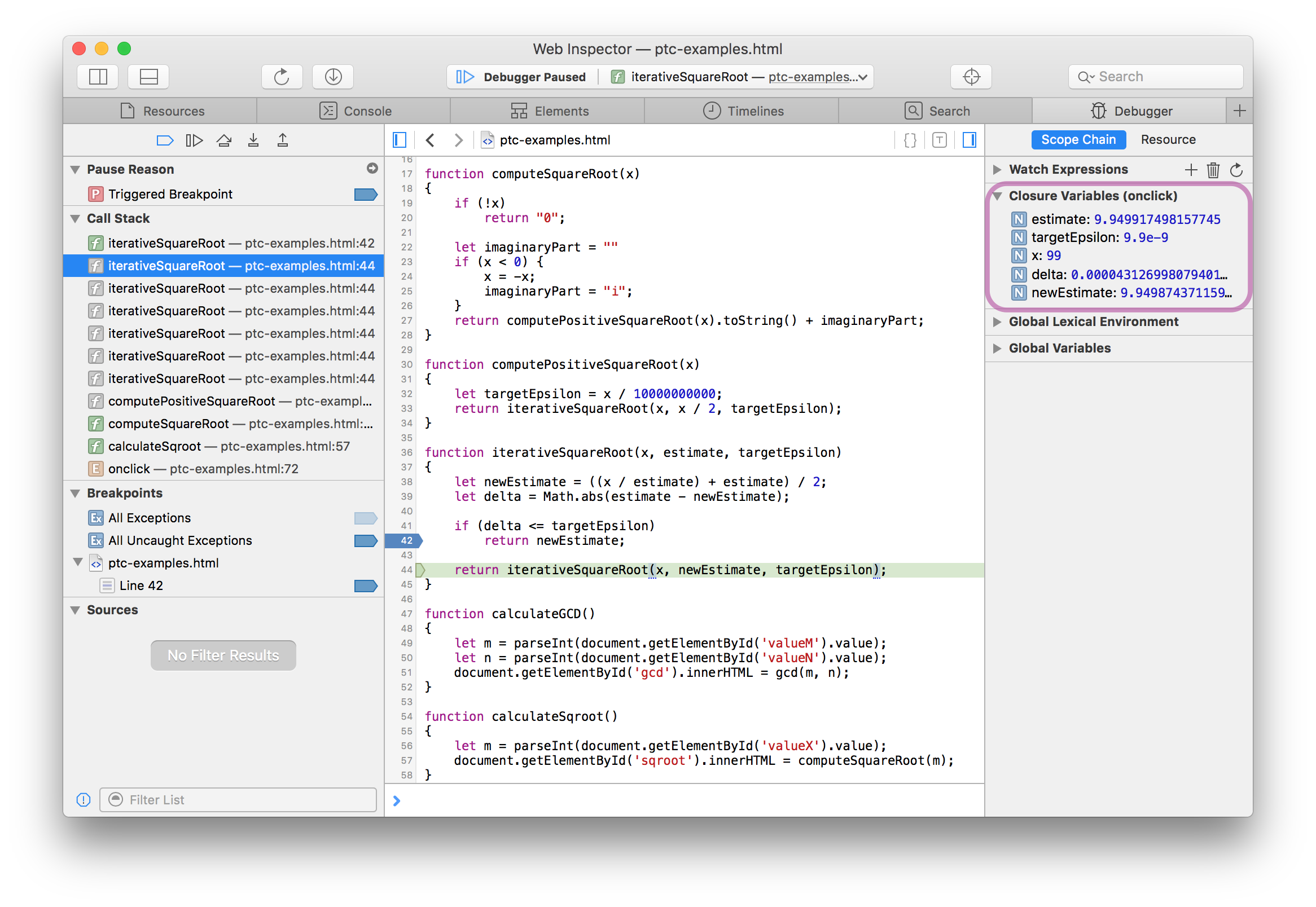
In this image, the local variables (circled) can be examined. The highlighted line in the program also shows where the tail deleted frame made a tail call from.

The next image shows what happens when single stepping from the breakpoint.

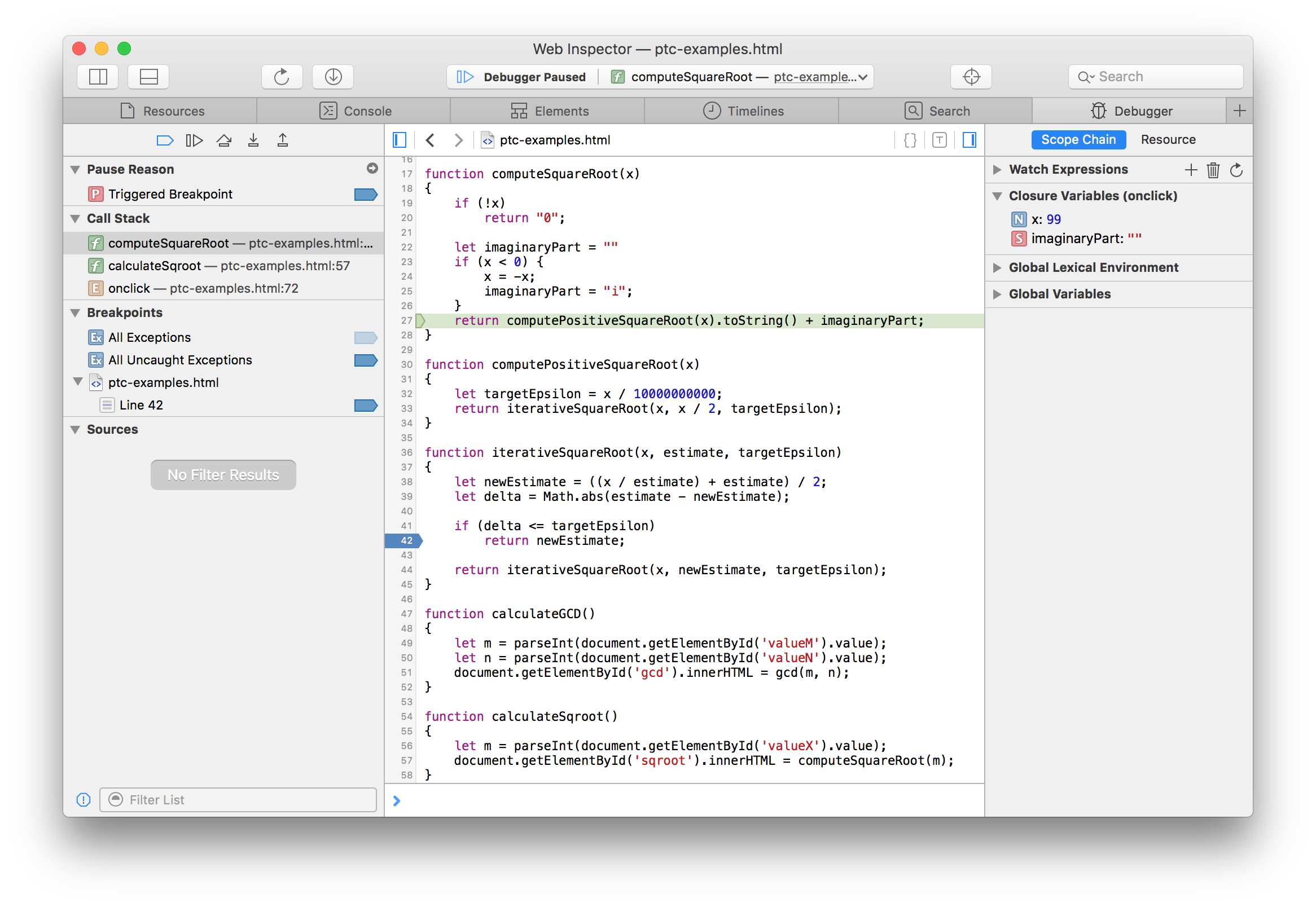
With on click of the step into button, Web Inspector now shows that we have returned directly to where computeSquareRoot() made the first tail call.

Summary

WebKit has ECMAScript 6 Proper Tail Calls and web developers are encouraged to take advantage of them to design programs in ways that were not possible before. Existing code can benefit as well. Web Inspector makes developing and debugging with PTC straightforward and intuitive.

The current Safari Technology Preview Release 4 has support for PTC. However, Web Inspector was only recently hooked up to work with ShadowChicken and therefore it is not in Safari Technology Preview Release 4. It is expected to be in the next Safari Technology Preview release. You can also try out ShadowChicken in Web Inspector by using a WebKit Nightly build.

Acknowledgements

This article was cowritten with Saam Barati from the JavaScriptCore team. We invite comments and feedback on WebKit’s PTC implementation. Feel free to get in touch with @msaboff, @saambarati, and @jonathandavis on Twitter.