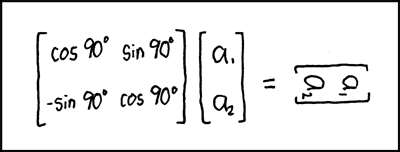The CSS3 matrix() Transform for the Mathematically Challenged

The CSS3 transform property can do some really cool things - with it, web designers can rotate, scale, skew and flip objects quite easily. However, in order for deisgners to have fine-grained, pixel level control over their transforms, it would be really helpful to understand how the matrix() function works. With the matrix() function, designers can position and shape their transformations exactly where they want to.

The problem is, not many people actually understand what the numbers in the matrix filter actually mean. To solve this issue, I have created a tool, which I call the CSS3 Matrix Construction Set that can take any block-element, positioned anywhere on the page, transform it anywhere else on the page using the matrix() filter, and reveal the correct CSS code for this operation. Look at the tool now and if that is all you are interested in, you can stop there. However, if you what to know what the numbers in the matrix() function actually mean, and why you want such knowledge in the first place, read on. I'll try to explain this as simply as possible (and please feel free to use the feedback form if you have any opinions on how to make this article better).

Matrices: Why Should I Care?

Matrices are to transforms like RGB hex codes are to colors: they are representations that are easy for computers to understand, but not human beings. Sure, web designers can use the rotate(), skew(), scale() and translate() functions to fulfill their transformation needs ... why should we bother with matrix() at all? There are a few cases when you may want to:

Brevity:

Using matrices, it is possible to represent a complex string of 2D transforms like this:

#object {
    transform-origin: 0 0;
    transform: rotate(15deg) translateX(230px)  scale(1.5, 2.6) skew(220deg, -150deg) translateX(230px)
}

using one matrix() rule like this:

#object {
    transform-origin: 0 0;
    transform: matrix(1.06, 1.84, 0.54, 2.8, 466px, 482px)
}

(Note: I have ignored the vendor-specific variants (e.g. moz-transform, etc.) for the sake of brevity).

Pixel-Perfection:

If you know exactly how you want your transformation to look, it'll take a bit of fiddling around to get it to look how you want using the other transform functions, and it may not be pixel perfect if you lack patience (like I do). However, using a tool like the Matrix Construction Set, you can place the transform exactly where you want (This is analogous to using a color wheel to choose RGB colors for you, instead of using keywords like red, green or peachpuff).

JavaScript:

Revealing an object's transform information using JavaScript's getComputedStyle() function will yield a matrix() function in all current web browsers that support CSS3 transforms, even if it was rendered using other transform functions like rotate(). For example, the object below has been rotated 45° using transform: rotate(45deg):

This object has been rotated 45°

But this link, which shows the object's computed style will reveal that internally it stores a matrix() function.

Ok, What Does The Markup Look Like?

The matrix() function takes 6 parameters in order for it to work:

#transformedObject {
     -moz-transform:    matrix(1.4488, -0.3882, 0.3882, 1.4489, 400px, -100px);
     -webkit-transform: matrix(1.4488, -0.3882, 0.3882, 1.4489, 400, -100);
     -o-transform:      matrix(1.4488, -0.3882, 0.3882, 1.4489, 400, -100);
     transform:         matrix(1.4488, -0.3882, 0.3882, 1.4489, 400, -100);
}

Note the difference with the Firefox implementation of matrix() — the last two elements need the px units after it. For now, think of it is a difference in notation, but we'll explain why this is later.

But What Do The Numbers Mean?

In order to explain what they mean, I will have to define a few math-concepts here. Don't panic if you are mathematically challenged. These concepts are not that hard to understand, but there is a bit of explanation needed. Why should you torture yourself if you hate math?

If you are a designer:

Think of the stuff below as informational. If you use the Matrix Construction Set you won't need to calculate anything by hand (but wouldn't you want to have an idea what the numbers mean anyway?)

If you are a JavaScript developer:

This information will be invaluable when optimizing scripts that rely on transformation effects. Just try to understand the basic concepts here, and if you still need help, use the Sylvester JavaScript library to do the heavy lifting for you.

If you want to be an über-geek:

All those matrix jokes you hear at parties will suddenly start to make sense!

Finally you'll be able to understand why all the geeks at work find this XKCD comic so funny.

Terminology

Matrix

The easiest way to think of a matrix is as a group of numbers written in a rectangle or square. For our purposes, we will be dealing with 3x3 matrices, such as this one below:

$\left(\begin{array}{ccc}1& 3& 5\\ 2& 4& 6\\ 0& 0& 1\end{array}\right)$

That's nine numbers! So how come the CSS3 matrix() function only has six?

#transformedObject {
     transform:  matrix(1, 2, 3, 4, 5, 6);
}

matrix(1, 2, 3, 4, 5, 6) = $\left(\begin{array}{ccc}1& 3& 5\\ 2& 4& 6\\ 0& 0& 1\end{array}\right)$

Dot Product

Next we are going to explain what a dot product is. At first, this may not seem like this is related to matrices at all, but I promise it does ... just read on and you'll understand why in no time. Trust me. :-)

Let's say you have two (x, y) points, $\left(\begin{array}{cc}1& 2\end{array}\right)$ and $\left(\begin{array}{cc}4& 5\end{array}\right)$. The dot product of these two points (written $\left(\begin{array}{cc}1& 2\end{array}\right)$ · $\left(\begin{array}{cc}4& 5\end{array}\right)$) is what you get when you multiply the two x-coordinates, multiply the two y-coordinates, and then add them together:

$\left(\begin{array}{cc}1& 2\end{array}\right)·\left(\begin{array}{cc}4& 5\end{array}\right)$ = 1x4 + 2x5 = 4 + 10 = 14

Got it? It's pretty simple, right? Note that when we write (x, y) co-ordinates like $\left(\begin{array}{cc}\mathrm{x}& \mathrm{y}\end{array}\right)$, we call $\left(\begin{array}{cc}\mathrm{x}& \mathrm{y}\end{array}\right)$ a vector. Vector notation can be written horizontally, (e.g. $\left(\begin{array}{cc}\mathrm{x}& \mathrm{y}\end{array}\right)$) or vertically (e.g. $\left(\begin{array}{c}\mathrm{x}\\ \mathrm{y}\end{array}\right)$). When using them in 2D transforms, we always add an extra co-ordinate with a number 1 at the end. So (20, 90) would be written $\left(\begin{array}{ccc}20& 90& 1\end{array}\right)$ or like $\left(\begin{array}{c}20\\ 90\\ 1\end{array}\right)$ in vector notation.

Multiplicatying a Matrix with a Vector

So, what does the dot product have to do with matrices? Well the idea of the dot product can also be extended to matrices. Let's say you need to multiply the following together:

$\left(\begin{array}{ccc}1& 3& 4\\ 2& 4& 5\\ 0& 0& 1\end{array}\right)$ · $\left(\begin{array}{c}20\\ 30\\ 1\end{array}\right)$

$\left(\begin{array}{ccc}1& 3& 4\\ 2& 4& 5\\ 0& 0& 1\end{array}\right)$ · $\left(\begin{array}{c}20\\ 30\\ 1\end{array}\right)$ = $\left(\begin{array}{c}1\times 20+3\times 30+4\times 1\\ \mathrm{.}\\ \mathrm{.}\end{array}\right)$ = $\left(\begin{array}{c}20+90+4\\ \mathrm{.}\\ \mathrm{.}\end{array}\right)$ = $\left(\begin{array}{c}114\\ \mathrm{.}\\ \mathrm{.}\end{array}\right)$

$\left(\begin{array}{ccc}1& 3& 4\\ 2& 4& 5\\ 0& 0& 1\end{array}\right)$ · $\left(\begin{array}{c}20\\ 30\\ 1\end{array}\right)$ = $\left(\begin{array}{c}115\\ 2\times 20+4\times 30+5\times 1\\ \mathrm{.}\end{array}\right)$ = $\left(\begin{array}{c}115\\ 40+120+5\\ \mathrm{.}\end{array}\right)$ = $\left(\begin{array}{c}115\\ 165\\ \mathrm{.}\end{array}\right)$

$\left(\begin{array}{ccc}1& 3& 4\\ 2& 4& 5\\ 0& 0& 1\end{array}\right)$ · $\left(\begin{array}{c}20\\ 30\\ 1\end{array}\right)$ = $\left(\begin{array}{c}115\\ 165\\ 0\times 20+0\times 30+1\times 1\end{array}\right)$ = $\left(\begin{array}{c}115\\ 165\\ \mathrm{0\; +\; 0\; +\; 1}\end{array}\right)$ = $\left(\begin{array}{c}115\\ 165\\ 1\end{array}\right)$

So, How Does This Relate To CSS3 Transforms?

#transformedObject {
     position: absolute;
     left: 0px;
     top: 0px;
     width: 200px;
     height: 80px;
     transform:  matrix(0.9, -0.05, -0.375, 1.375, 220, 20);
     transform-origin: 0 0;
}

What is the end result? Well, first let's take a look at the object without the transform CSS:

When the browser applies the transform to this block, it takes the matrix and multiplies it to each of the corner coordinates. For example, taking the bottom-right corner, (200, 80) or $\left(\begin{array}{c}200\\ 80\\ 1\end{array}\right)$, we get:

Let's look at the results for the other three coordinates. For (200, 0):

For (0, 80) test:

And finally, for (0, 0):

Here is the result:

I don't expect anyone to calculate these by hand on a regular basis (I personally don't). But now you know what these numbers mean. :-)

What About Internet Explorer?

Although transform-origin doesn't work with IE, it is possible to generate the matrix in another browser and use cssSandpaper to generate the shape of the transform in that browser. In order to fix the positioning, one can use Paul Irish's conditional stylesheet fix to position that block manually in IE only (it is what I used on this page so that the matrix transform in my example above appeared correctly in IE). I hope to have transform-origin working in cssSandpaper soon so that it will be unnecessary to do this.

Other Interesting Facts About Matrices

1. All the other CSS3 transform functions have equivalent matrix notation:

   scale(a)	scaleX(x)	scaleY(y)	translateX(x)	translateY(y)	translate(x,y)
   $\left(\begin{array}{ccc}\mathrm{a}& 0& 0\\ 0& \mathrm{a}& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}\mathrm{x}& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1& 0& 0\\ 0& \mathrm{y}& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1& 0& \mathrm{x}\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& \mathrm{y}\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1& 0& \mathrm{x}\\ 0& 1& \mathrm{y}\\ 0& 0& 1\end{array}\right)$

   skewX(x)	skewY(y)	skew(x,y)	rotate(θ)
   $\left(\begin{array}{ccc}1& tanx& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1& 0& 0\\ tany& 1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}1& tanx& 0\\ tany& 1& 0\\ 0& 0& 1\end{array}\right)$	$\left(\begin{array}{ccc}cos\theta & -sin\theta & 0\\ sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right)$

2. A list of transforms in CSS3 like this:

   #o1 {
      transform-origin: 0px 0px;
      transform: rotate(15deg) translateX(230px) scale(1.5);
   }
   

   is the same as multiplying the equivalent matrices together:

   $\left(\begin{array}{ccc}cos\mathrm{15°}& -sin\mathrm{15°}& 0\\ sin\mathrm{15°}& cos\mathrm{15°}& 0\\ 0& 0& 1\end{array}\right)$ · $\left(\begin{array}{ccc}0& 0& 230\\ 0& 0& 0\\ 0& 0& 1\end{array}\right)$ · $\left(\begin{array}{ccc}1.5& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$

   (I know, I didn't tell you how to multiply matrices together. Stephan Waner has written a good tutorial for matrix multiplication if you are interested.)
3. CSS3 2D-Transforms can only transform blocks into parallelograms. For example, it is impossible to transform a block into this shape:
   
   In order to do this, one must use CSS3 3D Transforms. This is why the Matrix Construction Set only has three control points to drag around, not four. If you would like to see a version of the Matrix Construction Set to use matrix3d(), please let me know by leaving a comment below.

In Conclusion

I don't expect anyone to be an expert in matrix artithmetic after reading this article. But at least you know what those pesky numbers mean, and this information may become useful in the future.

Acknowledgments

• The MathML markup used to display the mathematical equations in this article were rendered by MathJax, an excellent open-source JavaScript library
• The equations on this Physics Forum post was quite helpful in the creation of the Matrix Construction Set.
• The Matrix Construction Set uses the Sylvester JavaScript library written by James Coglan for performing matrix calculations. It also used my own DragDropHelpers library to smooth out the different browser implementations of HTML5 Drag and Drop.
• A blog post that has a bunch of math equations on it may be scary for web designers. My apologies.