Last week, Mike Malone, CTO of Betable, wrote a very insightful and informative article on Math.random() and PRNGs in general. Mike pointed out V8/Chrome used a pretty bad algorithm to generate random numbers and, since this week, V8 uses a better algorithm.
The article also mentioned the RNG we use in Firefox (it was copied from Java a long time ago) should be improved as well. I fully agree with this. In fact, the past days I've been working on upgrading Math.random() in SpiderMonkey to XorShift128+, see bug 322529. We think XorShift128+ is a good choice: we already had a copy of the RNG in our repository, it's fast (even faster than our current algorithm!), and it passes BigCrush (the most complete RNG test available).
While working on this, I looked at a number of different RNGs and noticed Safari/WebKit uses GameRand. It's extremely fast but very weak. (Update Dec 1: WebKit is now also using XorShift128+, so this doesn't apply to newer Safari/WebKit versions.)
Most interesting to me, though, was that, like the previous V8 RNG, it has only 32 bits of precision: it generates a 32-bit unsigned integer and then divides that by UINT_MAX + 1. This means the result of the RNG is always one of about 4.2 billion different numbers, instead of 9007199 billion (2^53). In other words, it can generate 0.00005% of all numbers an ideal RNG can generate.
I wrote a small testcase to visualize this. It generates random numbers and plots all numbers smaller than 0.00000131072.
Here's the output I got in Firefox (old algorithm) after generating 115 billion numbers:
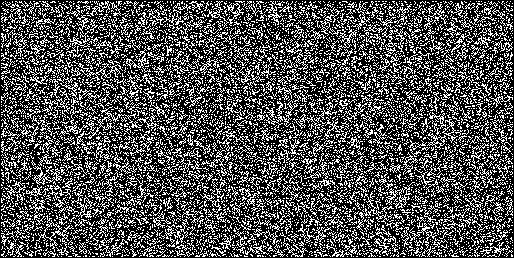
And a Firefox build with XorShift128+:
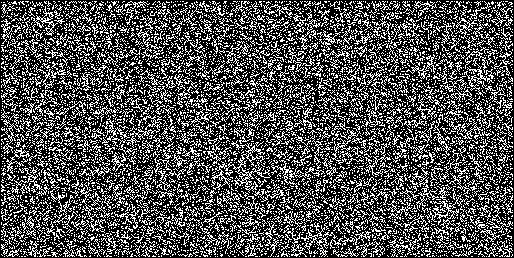
In Chrome (before Math.random was fixed):

And in Safari:

These pics clearly show the difference in precision.
Conclusion
Safari and older Chrome versions both generate random numbers with only 32 bits of precision. This issue has been fixed in Chrome, but Safari's RNG should probably be fixed as well. Even if we ignore its suboptimal precision, the algorithm is still extremely weak.
Math.random() is not a cryptographically-secure PRNG and should never be used for anything security-related, but, as Mike argued, there are a lot of much better (and still very fast) RNGs to choose from.